continuarea studiului

Am mai spus-o, dar altfel: in ultimul timp revin putin jenat la chestiunea atractorilor tocmai fiindca la un moment dat renuntasem cu naduf la ea, asa cum renunti la o idee nu atit proasta, cit slaba. Sint insa un oportunist fara scrupule :-) , in sensul descris de Einstein. Asa incit, demersul continua.

Am lucrat si astazi, chiar daca nu foarte mult, insa in zilele urmatoare, daca nu apar schimbari importante de agenda, voi fi, cred, in stare sa construiesc pulsul pe care-l vinez de citva timp. Treaba e destul de incurcata, fiindca in evolutia sistemului meu neliniar apar cel putin doua treceri de la un tip de comportare la altul. Stiu, suna criptic, insa detaliile ramin pe altadata. La descrierea sumara a evolutiilor din zilele urmatoare nu voi renunta.

M-am lamurit inca o data: modelul cu atractor e un soi de veriga lipsa, iar in matematica, atunci cind se intimpla asta, inseamna ca esti pe drumul cel bun. Asta-i si da forta ideii pe care am considerat-o acum sapte ani slaba, desi i-am dedicat atunci mai multe luni de lucru concentrat. Mai mult insa, pare a fi o prelungire naturala a ideii de puls acceptata in mecanica cuantica devenita deja clasica. Totusi, daca pulsul nu e analizabil fourier, iar asta nu pot verifica decit dupa ce l-am construit, atunci sint in incurcatura. Chiar verificarea in cauza ar putea deveni o problema datorita unor detalii legate de precizie, pulsul fiind, din cite pot sa-mi dau eu seama acum, unul foarte ingust. Din punct de vedere fizic, aceasta-i o calitate iesita din comun, matematic insa, poate fi un impediment major, calculele numerice fiind ingreunate.
Nu mai speculez, ramine de vazut ce forma va avea pulsul.

Cind lucrurile se complica...

Well, some mathematics problems look simple, and you try them for a year or so, and then you try them for a hundred years, and it turns out that they're extremely hard to solve. There's no reason why these problems shouldn't be easy, and yet they turn out to be extremely intricate. The Last Theorem is the most beautiful example of this. Andrew Wiles

Uneori ma gindesc, revenind la complexitatea stiintei moderne, mai ales la cercetarile de virf din domeniul fizicii teoretice, ca lipseste ceva fundamental daca lucrurile s-au complicat asa. Ca orice om preocupat de matematici, am invatat de timpuriu ca, de multe ori, atunci cind o rezolvare se complica mai mult decit ar fi cazul, ceva nu e in regula. Pe de alta parte, nu se stie prea bine ce inseamna ca o demonstratie se complica mai mult decit ar fi cazul. Fiindca atunci cind e vorba de conjecturi problematice care persista, nimeni nu poate sti cit ar fi cazul sa fie de complicata demonstratia, si, pina la urma, ceea ce conteaza cel mai mult este sa se stie daca o afirmatie este adevarata, si asta indiferent de lungimea demonstratiei. Mai mult, rezolvarea complicata a unei probleme poate fi corecta -- vezi, de pilda, ultima teorema a lui Fermat si demonstratia finalizata, ce-i drept, cu peripetii (in 1995), data pe citeva sute de pagini de Andrew Wiles: mai intotdeauna apar si alte rezolvari mai simple si mai ingenioase, dar care beneficiaza de rezultate sau descoperiri ulterioare. Ce-i drept, in cazul Wiles, problema nu se pune deloc asa: pentru a obtine demonstratia, el a trebuit sa inoveze masiv, nu atit sa dezvolte noi ramuri in matematicile moderne, cit sa lege domenii care pareau complet diferite, si asta, sprijinindu-se pe rezultatele multor matematicieni de virf.

Poti crea insa multa matematica de virf fara vreo legatura cu fizica, si, din cite imi pot da seama, in fizica, ceea ce am afirmat legat de complexitate se sustine in mod sistematic: atunci cind lucrurile se complica, nu doar ca ceva nu e in regula, dar putem vorbi de o oportunitate: in orice caz, de un bun prilej de a inova, de a gasi noi instrumente matematice, tocmai pentru ca lipseste ceva fundamental. Cam asta e ideea.

Do not worry too much about your difficulties in mathematics, I can assure you that mine are still greater. Albert Einstein

Si fiindca am amintit de Andrew Wiles, nu ma pot abtine sa preiau iarasi citeva link-uri de la youtube: am vazut chiar zilele trecute ca exista riscul ca fisierele video la care se face o referinta sa fie sterse la un moment dat. Dar in cazul asta merita sa imi asum riscul.

Fermat's Last Theorem - 1/5


Fermat's Last Theorem - 2/5


Fermat's Last Theorem - 3/5


Fermat's Last Theorem - 4/5


Fermat's Last Theorem - 5/5

In centrul galaxiei noastre exista...

... o GAURA NEAGRA.

"Avem, de asemenea, unele dovezi ca in centrul galaxiei noastre exista o gaura neagra mult mai mare, cu o masa de circa o suta de mii de ori mai mare decit aceea a soarelui."
-- Stephen Hawking (1987)

Intr-adevar, observatiile si masuratorile facute in ultimii ani arata ca singura explicatie pentru ceea ce se intimpla in centrul galaxiei noastre este ca acolo se afla o gaura neagra imensa, avind de cca 3 mln de ori masa soarelui.
Imaginati-va, stele de dimensiuni uriase orbiteaza ca niste biete planete in jurul unui obiect imens care se afla in centrul galaxiei noastre si care nu poate fi altceva decit o gaura neagra.
Mai mult, s-ar parea ca in centrul fiecarei galaxii exista cite o gaura neagra uriasa.

Pentru detalii, se poate urmari documentarul Monster of the Milky Way de la PBS (sint nevoit sa dau link-ul direct: din pacate, variantele de pe youtube nu sint sigure; cele de saptamina -- vezi postarile referitoare la miniseria The Elegant Univers -- au fost eliminate din serverele youtube chiar de catre administratorii site-ului din motive legate de drepturile de utilizare/difuzare). Script-ul MMW se gaseste aici.




Andrea Ghez este unul dintre liderii cercetarilor privind centrul galaxiei: merita sa cititi biografia ei (click pe imagine).

revenire la model

Rezultatele cercetarilor de teoria cuantica a cimpului trebuie sa duca la ecuatii neliniare. Doar acestea pot descrie interactia dintre particule, crearea si anihilarea acestora: ecuatiile liniare pot descrie o particula sau mai multe, pachetele de unde corespunzatoare se compun, dar nu interactioneaza, asa cum se intimpla in realitate. Desigur, pina la o asemenea teorie e inca o cale lunga. Eu mi-as dori sa stiu macar cu ceva mai mult despre o particula: de pilda motivul pentru care aceasta isi pastreaza structura si daca se poate vorbi de ea ca despre o manifestare neliniara a spatiului gol -- i.e. vid, despre care se afirma adesea ca "raspunde" neliniar. Einstein spune la un moment dat:

"Totusi, ecuatiile lui Maxwell nu permiteau derivarea acelui echilibru al electricitatii ce constituie o particula. Numai alte ecuatii, ecuatiile neliniare ale cimpului puteau eventual sa realizeze asa ceva. Nu exista nici o metoda pentru gasirea unor asemenea ecuatii ale cimpului care sa nu fie expusa alunecarii intr-un arbitrar aventuros."

Asadar, chiar doar pentru descrierea fidela a unei singure particule sint necesare ecuatii neliniare -- multi cauta direct ecuatiile de cimp care sa descrie interactia dintre particule fara a avea ecuatiile neliniare corespunzatoare acestora.
Intrebarea care survine imediat este: in ce sens poate fi o particula manifestarea neliniara a spatiului gol?

Ramine de vazut daca modelul pe care-l studiez poate genera in mod neliniar un puls care sa fie analizabil fourier: in orice caz, nu stiu inca daca aici se poate vorbi chiar de o echivalenta, drumul fiind cu sens unic. Am mai intii o descriere neliniara, iar aceasta duce la una liniara; nu invers. Si chiar daca ar fi vorba de o echivalenta, nu cred ca este de acelasi tip cu aceea care identifica de pilda doua numere cu suma lor. Ar fi insa interesant de aflat daca exista si alte ecuatii neliniare care sa aiba acelasi rezultat.
Ceea ce stiu cu siguranta inca de pe acum este ca, desi componentele pulsului ipotetic "asculta" de regula superpozitiei ca la pulsul fourier clasic, spre deosebire de componentele unui puls fourier clasic acestea interactioneaza neliniar.

It seems hard to look at God's cards. But I cannot for a moment believe that he plays dice and makes use of 'telepathic' means as the current quantum theory alleges He does. Einstein

Bohr to Einstein: "Einstein, stop telling God what to do!"

din nou atractori

Am lucrat toata ziua la o idee mai veche; aceea prin care, utilizind aproximari si atractori, sa generez neliniar pulsuri/perturbatii analizabile fourier. Inca nu am construit in acest mod o perturbatie (i.e. un puls), dar modelul pare promitator.

Ce-i drept, atractorii au cazut cumva in dizgratie din momentul in care am hotarit ca ma intereseaza in primul rind ordinea: treptat, am revenit la modelele slab haotice ale mecanicii clasice (din 2003 m-am concentrat destul de mult asupra sistemelor mecanicii hamiltoniene: se stie, sistemele hamiltoniene nu au atractori, acestia din urma caracterizind mai degraba sistemele cu haos tare).

Astazi nu am facut decit sa reiau un model pe care l-am studiat intens acum sapte ani. Am realizat, ca si atunci, ca fenomenul relevat nu apare decit in cazul atractorilor, in plus, ma atrage caracterul puternic neliniar al modelului -- multa lume admite azi ca la o scara foarte mica, in imediata vecinatate a unei particule elementare cimpurile sint foarte intense --, dar si faptul ca ar putea constitui o alternativa neliniara la compunerea/integrala fourier care e o transformare liniara.
Mai exista cel putin o trasatura interesanta: una ar fi aceea ca modelul ia nastere in mod natural din aproximari. Or, in cautarea originii constantei lui Planck, aproximarile sint inevitabile, ceea ce sugereaza ca intr-un model reusit, ele ar putea chiar sa aiba contributia lor. O alta trasatura importanta a modelului -- iar asta mi-o sugereaza pur si simplu flerul --, ar fi aceea ca, fara calculator, ar fi imposibil de pus in evidenta, calculele fiind monstruoase. Ce inseamna asta? Inseamna o sansa in plus pentru mine: toate cercetarile actuale se fac mai degraba de catre fizicieni cu background si abilitati matematice iesite din comun (la Harvard, Princeton, Columbia, Stanford, s.a.m.d.), insa la nivelul unor calcule mai degraba formale -- se utilizeaza chiar software puternic, dedicat acestor manipulari formale --, experimentul numeric jucind inca un rol minor, fiind practic neglijat. Cum nici background-ul si nici abilitatile mele matematice nu se compara cu ale celor care studiaza teoriile superstring-urilor, experimentele numerice ingenioase bazate pe o intuitie fizica sanatoasa ramin singura mea sansa. Desigur, in cazul unor rezultate, simplitatea nu ar fi deloc de neglijat: in orice caz, un asemenea model nu se compara ca dificultate cu cel furnizat de teoriile suprestring-urilor (experienta uimitoare a lui Einstein confirma faptul ca o teorie poate fi cu-adevarat revolutionara daca e relativ simpla: teoria speciala a relativitatii putea fi explicata inca de atunci cu destula usurinta celor care studiau in primii ani la facultatile de matematica/fizica).
Trasatura cea mai importanta a modelului ramine insa aceea ca se admite (pe mai departe) valabilitatea principiului superpozitiei (i.e. combinatia liniara a doua solutii este tot o solutie), principiu esential pentru mecanica cuantica.

Lucrurile se leaga intru citva: incepind din 2003 am creat un model neliniar cu doua grade de libertate care dadea nastere la pulsuri. M-am putut lamuri atunci la modul practic cum sistemele neliniare cu un numar finit de grade de libertate pot fi echivalate cu unele liniare cu un numar infinit de grade de libertate. Evident, avind de-a face direct cu pulsuri, nu am fost nevoit sa apelez la transformari sofisticate cum ar fi aceea data de ecuatia Frobenius-Perron. Problemele modelului din 2003 au fost tot timpul lipsa de localizare a pulsului odata cu scaderea coeficientului de neliniaritate si caracterul (pregnant) discret al transformatei sale fourier: particulele libere au spectru continuu.

Am motivat ceva mai devreme renuntarea la modelul din 2000, insa ar mai fi citeva detalii de lamurit aici: pe-atunci nu mi-era aproape matematica ceva mai pretentioasa a pulsurilor complexe, in plus, detaliile legate de constructia unor astfel de perturbatii imi apareau suficient de complicate pentru a ma descuraja -- ar fi suficient poate sa mentionez aici ca spatiul hilbert asociat are dimensiunea foarte mare, de ordinul miilor sau zecilor de mii. Nu am procedat asa cum procedez in situatiile de acest fel cind las modelul in asteptare incercind sa epuizez alternativele (ce par) mai simple sau mai plauzibile, fiindca atunci am studiat mai departe manifestarile care mi s-au parut interesante: printre altele, am incercat chiar sa gasesc circumstante simplificate in care dimensiunea sa fie mult mai mica. Renuntarea la model s-a produs insa treptat, pe masura ce deveneam constient de ineficacitatea lucrului cu probabilitati in studiul chestiunilor fundamentale. Am revenit periodic la model, parindu-mi-se ca are citeva proprietati cu totul remarcabile care ar merita fructificate matematic.

Inca mai cred si astazi ca este o fortare postularea caracterului probabilistic al amplitudinii functiei de unda -- obiectul central al studiului mecanicii undelor: presupun pur si simplu ca postularea nu era necesara. Fiindca mai cred si astazi ca daca am gasi teoria mult cautata, si daca probabilitatile ar fi cu-adevarat inevitabile in mecanica cuantica, atunci ele ar trebui sa rezulte in mod natural din teorie. Ca sa duc rationamentul pina la capat, trebuie sa constat un lucru surprinzator, totusi cunoscut: singurul domeniu matematic din care decurg in mod natural probabilitati este cel care astazi se ocupa de haos, mai precis de haosul determinist (rezultat din studiul ecuatiilor diferentiale sensibile la conditia initiala), atractori, s.a.m.d. -- chiar si sisteme hamiltoniene, unde vorbim, ce-i drept, despre haos slab (v. M.C. Gutzwiller).

In legatura cu modelul, astazi am vazut lucrurile ceva mai clar: suficient de clar pentru a realiza ca, desi atunci am ajuns sa construiesc sistemul respectiv pornind de la un lant markov cu timp continuu, adica postulind probabilitati, postularea lor putea fi evitata cu usurinta. Evident, nu ma refer la posibilitatea banala ca probabilitatile dintr-un graf sa fie asimilate cu o marime fizica ce se conserva (cu energia, de pilda), ci pur si simplu la faptul ca se poate ajunge la aceleasi rezultate fara a se recurge la studiul unor lanturi markov. Eram insa constient ca asa stau lucrurile fiindca inca de pe atunci am scris citeva programe de testare a acestei ipoteze.

Pentru cei care nu sint familiarizati cu domeniul, poate parea surprinzator ca probabilitatile sa decurga natural din sisteme de ecuatii prin excelenta deterministe. Diagrama de bifurcatie de mai jos rezulta in urma rezolvarii unui asemenea sistem: arata intr-adevar spectaculos.

interviu cu Brian

Iata aici un interviu mai vechi cu Brian Greene. Il postez fiindca este destul de interesant dar si pentru ca pica bine dupa mini-seria prezentata aceste zile pe blog.

III. Welcome to the 11th Dimension

Transcriptul este aici.

Welcome to the 11th Dimension 1


Welcome to the 11th Dimension 2


Welcome to the 11th Dimension 3


Welcome to the 11th Dimension 4


Welcome to the 11th Dimension 5

II. String's The Thing

Transcriptul este aici.

String's The Thing 1


String's The Thing 2


String's The Thing 3


String's The Thing 4


String's The Thing 5

I. Einstein's Dream

Probabil ca multi au vazut documentarul the Elegant Univers prezentat de, si facut dupa cartea lui Brian Greene. Merita revazut chiar daca nu credeti in povestea asta cu string-urile (teoria string-urilor).
Referintele istorice sint uneori destul de slabe si la nivel anecdotic (vezi Newton si marul). Exista insa si multe observatii interesante pe care le face de regula un cercetator autentic -- v. mai ales cele referitoare la unificare.
Serialele pot fi urmarite pe site-ul pbs, inconvenientul fiind acela ca sint prea scurte.
Astazi prezint serialele primei ore, miine le voi prezenta pe cele din ora a doua, iar poimiine pe cele din ora a treia. Poate unii doresc urmarirea textului simultan cu derularea documentarului: transcriptul poate fi gasit aici.

Einstein's Dream 1


Einstein's Dream 2


Einstein's Dream 3


Einstein's Dream 4


Einstein's Dream 5

reasezare

Revin la un ritm de postare ceva mai lent. Nu de alta, dar am nevoie de timp. Voi incerca sa postez zilnic, insa doar daca am ceva de spus. Inca ma incoltesc vreo citeva idei legate de studiile referitoare la contextul geometric al aparitiei constantei lui Planck. Activitatile de felul asta sint extrem de cronofage, sint insa printre putinele care ma atrag. Sint zile intregi cind numai asta fac: gindesc, gindesc si iar gindesc la diversele modele matematice. Cautarile acestea sint in mare masura sterile, de aceea si aduc intru citva cu acelea ale cautatorilor de aur.
Einstein avertiza odata:

"Pentru cel ce se straduieste sa realizeze o opera stiintifica sansele de a ajunge la un rezultat de valoare sint foarte slabe, chiar daca este foarte inzestrat..." (A. Einstein, Correspondance, p.77)

Am si un sentiment de insatisfactie datorat inexistentei unor site-uri romanesti de stiinta consistente. Toate cele pe care le-am vazut pina acum sint amatoricesti si simpla lor parcurgere te umple de melancolie.
In rest, unde intorci capul, cancan, politica, afaceri dubioase, ziare cvasi-tabloidizate, personalitati in deriva, monoloage, lipsa dezbaterii autentice de orice fel, multa religie si fotbal, paseism cu fason cultural si foarte foarte putina stiinta sau chiar deloc. Si cind ma gindesc ca sint destui carora le place atmosfera asta, chiar ca devin melancolic.

Nu exista remediu decit in afara, la cei care sint interesati cu-adevarat de universul acesta mare: ma numar si eu printre cei care cred ca nu putem afla mare lucru despre noi daca nu stim cu mult mai multe despre legile naturii.
De aceea merita poate sa rememoram povestea dramatica a descoperirii facute de unul dintre cei mai mari savanti, Stephen Hawking. Am mai spus-o, unii dintre noi ne folosim de toata libertatea pentru a gasi adevarul: altii se folosesc de adevar pentru a se elibera.

Cel care a luat in serios inca de la inceput problema paradoxului informatiei (pierderea informatiei intr-o gaura neagra sustinuta chiar de catre Hawking) este Leonard Susskind, unul dintre parintii teoriei superstring-urilor, si unul dintre cei mai interesanti ginditori ai momentului. El a dezvoltat practic o idee remarcabila a lui Gerardus 't Hooft, aplicabila fenomenelor cuantice, aceea a principiului holografic, potrivit caruia informatia corespunzatoare fenomenelor care au loc intr-un volum se regaseste pe o suprafata care delimiteaza acel volum -- in cazul nostru, e vorba de orizontul evenimentelor gaurii negre. Se stie, gaurile negre au devenit deosebit de interesante din punct de vedere teoretic tocmai datorita caracterului lor special: fiind foarte masive, sint studiate cu ajutorul teoriei generalizate a relativitatii, dar, in acelasi timp, fiindca spatial sint foarte restrinse (mici), nu pot fi evitate efectele/manifestarile cuantice, si deci nici aplicarea mecanicii cuantice. Cum toate teoriile de unificare se lovesc de aceasta limita clasic-cuantic (teoria lui Einstein fiind una considerata clasica), gaurile negre au fost studiate asiduu tocmai pentru a se clarifica raporturile in care se afla teoriile clasice si cele cuantice. Juan Maldacena este cel care i-a furnizat argumentele matematice riguroase lui Leonard Susskind, argumente care aratau ca informatia nu se pierde, cum sustinea Hawking.

Partea I


Partea a II-a


Partea a III-a


Partea a IV-a


Partea a V-a

prejudecati legate de matematica

Din punctul de vedere al lui Einstein, demersul stiintei nu era atit lupta cu prejudecatile, cit gasirea, determinarea lor: fiindca acestea sint atit de bine asimilate, incit nu mai sint bagate in seama, fiind de la sine intelese, si deci acceptate ca atare.
Daniel Tammet. Poate ca tot nu va spune mare lucru nici macar dupa ce v-ati aruncat ochii pe referintele din wikipedia. Ei bine, acest om, nu doar ca are o memorie a numerelor fenomenala, dar are o relatie de un tip special cu acestea, o relatie afectiva. Nu te poti apropia asa de mult de un obiect mai degraba abstract fara a fi emotionat de armonia sa structurala. Daniel gindeste numerele in asociere cu forme. In adolescenta gindeam cumva similar, fiindca inca de atunci mi-am dat seama ca pentru a memora siruri mari de numere, acestea ar trebui asociate cu forme sau obiecte concrete. Pare o risipa, insa memoria noastra nu poate lucra altfel decit imaginativ.
Exista insa argumente matematice puternice cum ca acest principiu dupa care numerelor le corespund forme nu se rezuma doar la problematizarile noastre mnemotehnice mai mult sau mai putin arbitrare...
Nu sint mare amator de curiozitati, insa in ceea priveste numerele si felul in care oamenii le gindesc, am avut intotdeauna intrebari, mirari. Mai stiu ca unii dintre marii matematicieni au fost foarte buni la calculele brute pe care astazi noi am ajuns sa le evitam sistematic -- il amintesc aici doar pe Euler, care calcula tot asa cum respira: a avut, ce-i drept, si scaderi; printre altele, cu privire la numerele negative pe care nu le-a vazut ca pe o extindere naturala a multimii numerelor pozitive, a afirmat ca sint mai mari decit infinitul.

Contrar a ceea ce cred unii despre matematica, intuiesc ca memoria joaca un rol important chiar si in intelegerea acesteia.
Exista insa o alta prejudecata suparatoare, dupa care matematica inseamna intii de toate logica. Sir Atiyah o demonteaza fara dificultate, aratind ca doar in finalul rationamentelor sale matematicianul are nevoie de logica, demersurile obisnuite fiind unele de tip intuitiv si de imaginatie indelung si minutios cultivate. El spune:

"Well, the idea that mathematics is synonymous with logic is a great ridiculous statement that some people make. Mathematics is very difficult to define, actually, what constitutes mathematics. Logical thinking is a key part of mathematics, but it's by no means the only part. You've got to have a lot of input and material from somewhere, you've got to have ideas coming from physics, concepts from geometry. You've got to have imagination, you're going to use intuition, guesswork, vision, like a creative artist has. In fact, proofs are usually only the last bit of the story, when you come to tie up the... dot the i's and cross the T's. Sometimes the proof is needed to hold the whole thing together like the steel structure of a building, but sometimes you've stopped putting it together, and the proof is just the last little bit of polish on the surface.
So the most time mathematicians are working, they're concerned with much more than proofs, they're concerned with ideas, understanding why this is true, what leads where, possible links. You play around in your mind with a whole host of ill-defined things."

In documentar apare si Kim Peek, cel dupa care s-a inspirat filmul Rain Man (cu Dustin Hoffman)

Sir Atiyah spunea despre Ed Witten, cel mai bun teoretician al superstring-urilor in acest moment:
"... he has made a profound impact on contemporary mathematics. In his hands physics is once again providing a rich source of inspiration and insight in mathematics. Of course physical insight does not always lead to immediately rigorous mathematical proofs but it frequently leads one in the right direction, and technically correct proofs can then hopefully be found. This is the case with Witten's work. So far the insight has never let him down and rigorous proofs, of the standard we mathematicians rightly expect, have always been forthcoming."

Despre timp si urcusul catre izvoare

Desi combat mare parte din ideile crestine, nu sint fericit cu aceasta situatie. E drept, nici n-as avea curajul sa fac asta daca n-as simti un sprijin in afirmatiile fara echivoc ale lui Einstein.
Sa fie nostalgiile rele in sine? Marturia alegoriei pesterii ma incurajeaza de asemenea sa cred ca nu: exista o nostalgie care are ca subiect/obiect lumea platonica a ideilor, a adevarului, a preexistentului.

Cine oare nu e fermecat de linistea unei manastiri izolate? Si nu va este ciuda ca in modernitate am pierdut acest sentiment al firescului asezat? Sesizati desigur ca am devenit intre timp propriii nostri dusmani tocmai fiindca dorim sa ajungem propriii nostri stapini -- ne laudam cu asta: singura problema ramasa este aceea ca nu stim inca cine sintem.

Oamenii vechi pareau sa aiba tot timpul din lume iar noi am pierdut inclusiv acest sentiment sanatos al proprietatii timpului: scenariile montate in pestera se succed cu asemenea repeziciune incit nici scamatorii insisi nu mai prididesc cu avalansa de umbre. Ni se spune ca nu mai este timp, ca timpul e avere (sau ma rog, bani), nu invers: am fost deposedati pe negindite de timp.

Preexistentul, adevarul sint atemporale, doar umbrele lor fiind temporale. Scamatorii de serviciu insa ne-au adus in situatia de a crede ca temporalitatea este un atribut esential al ideilor. Invers, ni se pare ca sintem asimilati in mod utopic cu simplele idei atunci cind ni se refuza timpul, adica existenta. Umbrelor li se furnizeaza incontinuu timp, oamenilor nu. Ce sa insemne toate astea? Umbre nu sintem, caci spuneam ca umbrelor li se da timp: nu sintem insa nici idei, nu parem a fi atemporali.

Sintem spectatorii in lanturi nazuind sa devina scamatori. Asadar, nu incercam sa iesim, ci ne dorim postura de scamator care dispune de timp si care ii amageste pe ceilalti pentru a le hrani imaginarul cu umbrele timpului.
De ce am fost deposedati de timp? Pai deficitul de timp este cel care ne tine locului -- numai un om care are timp isi poate cauta iesirea --, iar prin timpul concentrat in miinile scamatorilor sint animate umbrele, i.e. concretul, superficialitatea.
Nu doar guvernantii, dar buna parte din elite deturneaza/risipesc timpul: fiindca il investesc in spectacolul de animatie. Astazi nici nu mai este necesar ca oamenii sa fie tinuti in lanturi, fiindca cei mai multi dintre ei au pierdut gustul ideilor, singuri refuzindu-si libertatea de a iesi la lumina. Aceasta fiindca le ajunge si se bucura de "libertatea" de a privi.

E o asociere comuna in textele filosofice aceea a umbrelor cu superficialitatea. Fara a face o exceptie, textul de fata aduce insa o completare punind o intrebare. Nu cumva printre umbrele respective regasim si prejudecatile, revelatiile si credintele de tot felul?

Religiile forteaza, postuleaza existenta unor fiinte transcendente si nici macar nu se rezuma doar la asta: in mod paradoxal, prin apelul ilicit si abuziv la imaginar (invierea, sfintii, ingerii) acestea nu devin mai mult decit (tot) niste simple umbre, reflexe ale transcendentului elementar. Mai este greu de inteles atunci de ce promotorii credintelor sint vazuti, la limita, ca niste simpli scamatori?
Stiintele si ratiunea pe de alta parte, nu se rezuma doar la transcendentul lumii platonice a ideilor, adevarului, preexistentului dar, fiind abia la inceput, acestea constituie obiectul demersului lor de moment, tropismul in cautarea luminii urmarind drumul catre iesire. La iesire nu poti ajunge doar cu gindul, ci pasind pur si simplu, avansind lent, depasind dificultatile de adaptare, adica din aproape in aproape.

Credinciosii mi-ar putea intoarce argumentul sustinind ca teoremele sint umbre, si nu credintele: istoria ne arata insa ca timpul este un factor hotaritor cind vorbim de religii, acestea nascindu-se, evoluind si disparind ca orice lucru trecator de pe lumea asta, criteriul de selectie raminind supravietuirea. Nu acelasi lucru este valabil in cazul teoremelor, acestea fiind adevarate in veacul veacului daca se respecta intocmai conditiile impuse in ipoteze. Pe de alta parte, transcendentul obiectelor matematice cu greu ar putea fi negat: conceptul de dreapta exista doar dincolo de simpla perceptie, in realitate neexistind drepte, ci doar umbre ale conceptului respectiv, sa le spunem aproximari. Pentru a ajunge la teoreme, criteriul de selectie care trebuie aplicat afirmatiilor este adevarul: numai daca producem o demonstratie valida a unei afirmatii putem fi siguri ca aceea este o teorema.

(De ce, asa cum sint teoremele echivalente daca luam in considerare criteriul adevarului, revelatiile nu pot fi echivalente, potrivit aceluiasi criteriu? Revelatiile unui calugar virtuos din zilele noastre nu sint acceptate a fi echivalente cu ale lui Iisus si nici macar cu ale lui Pavel.)

Visez la o vreme in care oamenii isi vor fi regasit si recuperat tot timpul din lume, si in care ei vor pasi incet si masurat, intr-o calma tensiune dar intr-o liniste semnificativa pe drumul catre iesire. Poate ca in acea vreme pacea din templele de astazi se va regasi mai ales in sufletele oamenilor.

Inc-o utopie? Nu. Fiindca lucrurile pot incepe sa se intimple inca de acum. Nu-i mai credeti pe aceia care fac apologia lipsei de timp: fiti contemporani cu Palton, cu Euclid... Nu va grabiti. Vi se ofera calatorii in locuri nemaivazute: refuzati-le. Nu exista calatorii mai intaritoare decit cele ale mintii in lumea ideilor, in cautarea adevarului. Asa cum sustinea Schrödinger, ideea nu e aceea de a vedea ceea ce inca n-a vazut nimeni, ci aceea de a gindi asa cum nu a gindit inca nimeni despre ceva ce vede toata lumea.

Complexitate vs dezordine

(alergare, 25 august 2007)
temperatura: 35-32 de grade
fereastra puls: 150-
timp in fereastra: 43’00’’
timp total: 58’00’’
puls maxim: 158
distanta: 12.7 km
itu: 79-80

Am un subiect care imi da tircoale de citeva zile, dar inca nu s-a acutizat, ca sa zic asa. Si de aceea nu voi insista acum prea mult asupra sa. E tipul de subiect care revine periodic, tocmai fiindca nu poate fi expediat prea usor, cerind noi idei si dezvoltari, adica timp.

Este vorba despre complexitatea stiintelor moderne, si ca exemplu pot fi luate matematicile si fizica teoretica.
Ei bine, nu vi se pare ciudat totusi ca acestea se complica in loc sa se simplifice? Se spune adesea ca unificarile simplifica tabloul conceptual al stiintei moderne. Totusi, pentru diletant, dar din pacate nu doar pentru el, nu este citusi de putin evident ca asa stau lucrurile.

Am ajuns in situatia paradoxala ca stiinta complica in loc sa simplifice: mai in gluma, mai in serios, intrebarea este; cum poti pretinde, de pilda, ca o formula sau un sistem de ecuatii explica un fenomen, daca fenomenul in sine pare mai usor de studiat decit formulele sau ecuatiile care-l descriu?

Exista, de asemenea, fapte care incurca si mai mult situatia.
Se stie, creierul este in timpul somnului in stari/atractori care pot fi modelate in spatii cu relativ putine dimensiuni, cinci sau sase. In stare de veghe insa, creierul pare ca evolueaza haotic, in orice caz, spatiile necesare pentru descrierea evolutiei sale au un numar infinit de dimensiuni. Totusi, omul poate cunoaste lumea in care se misca doar in stare de veghe. Cum se face atunci ca el observa regularitatile lumii fiind chiar el intr-o stare cvasi-haotica? Sa fie asta doar o aparenta, in realitate fiind vorba de o complexitate extrema a mintii sau exista vreun principiu inca necunoscut noua datorita constringerii caruia, un sistem nu poate pune in evidenta ordinea altuia decit dintr-o perspectiva/stare mai dezordonata (decit aceea a sistemului studiat)?

Ordine vs Haos, Cunoastere vs Credinta

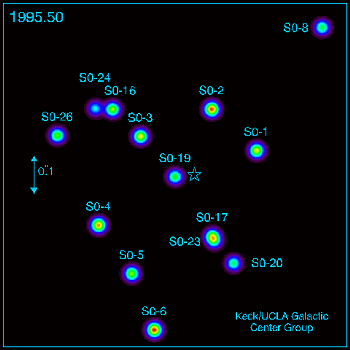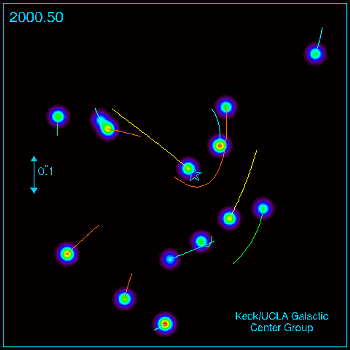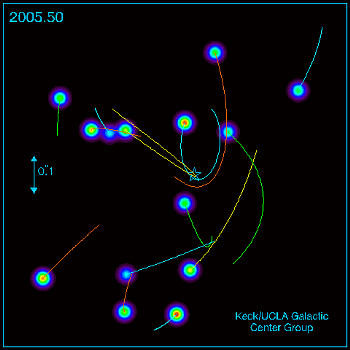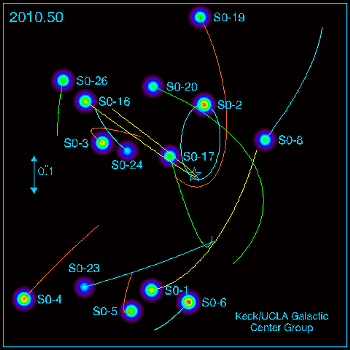
Controversa privind studiul ordinii sau al haosului/probabilitatilor in stiinta devine mai lamurita, as zice, daca privim ceea ce se petrece in fizica moderna din perspectiva sugerata de un fapt remarcabil: mecanica cuantica a cistigat la loto potul cel mare pe la inceputul secolului al XX-lea si, ca orice incepator in ale jocurilor de noroc, ar vrea in continuare sa cistige; ei bine, tot de la loto stim, nu poti cistiga in fiecare zi; de fapt cistigi o data in viata si chiar ceva mai rar.

Un om serios este insa acela care, fara a ignora fenomenul, nu devine totusi dependent de jocul de noroc, oricare ar fi acesta. E drept, pe de alta parte, ca darwinismul se sprijina pe ideea de diversitate si de sansa, iar darwinsmul este o teorie stiintifica in toata regula, daca nu chiar una dintre cele mai fericite descoperiri din toate timpurile; dar aici succesul survine din faptul elementar ca criteriul este supravietuirea si nu adevarul.
Mai mult, la nivel celular, miscarea browniana este aceea care face, se pare, viata posibila. Si, ca o incununare, principiul al doilea al termodinamicii reteaza in mod rational optimismul nejustificat afirmind ca fenomenele naturale tind catre starea de dezordine maxima, i.e. ordine minima. Exista oare exceptii?

Ceea ce nu ne spune nici darwinismul si nici o alta teorie -- nici macar cele furnizate de antropologie sau psihologie --, este cum anume devine posibila cunoasterea. Acceptam, in mod evident, ca pe ceva ce decurge din experienta posibilitatea cunoasterii sistematice a legilor lumii. Ei bine, cum anume ajunge mintea sa descopere regularitatile lumii si sa priceapa astfel ce se intimpla in lume si cu ea insasi?

Intr-un fel, desi sintem constienti de existenta sa, corpul nostru este un soi de transcendent pentru noi de vreme ce nu-l putem influenta in mecanismele sale fundamentale si mare parte din ceea ce se intimpla cu el ne este complet strain. In mod normal, nu putem influenta fin nici macar cele mai cunoscute manifestari ale sale. Aici poate fi luat drept exemplu incercarea de a influenta pulsul prin simpla vointa: direct, lucrul pare imposibil, putem insa alerga, si atunci pulsul creste ca efect al cresterii efortului, dar corpul hotareste singur care puls e mai potrivit unui anume ritm de miscare.

Iisus imi apare ca si matematicienii aceia care pretindeau ca au rezolvat o anumita problema dar ca nu au avut timpul/spatiul sa o noteze: in felul acesta pot lua nastere legendele de vreme ce unii dintre urmasi (in cazul nostru, Pavel) pot ajunge sa pretinda ca maestrul ar fi putut sa schiteze demonstratia, si ca daca a facut-o, intre timp s-a pierdut. In ceea ce priveste unele demonstratii, apare cu evidenta faptul ca ele nu puteau fi gindite/facute fara cunostinte mult mai avansate de matematica: asa este si cu invierea. In matematica, demonstratia trebuie sa poata fi refacuta ori de cite ori este necesar, tot asa cum, in fizica, rezultatul unui experiment trebuie sa se verifice/repete in mod sistematic.

In viata de toate zilele, noi ne jucam de-a invierea, o mimam anual, desi ea nu are loc. Ce fel de teorie este aceasta, in care afirmatiile nu pot fi nicicum verificate dar consecintele ei sint mimate? Nu ar trebui oare sa invie macar discipolii, sau cei care urmeaza credinta (in aceasta stranie teorie)?

Cum ar fi daca matematica nu s-ar baza pe afirmatii care sa aiba demonstratii oricind si oriunde verificabile, ci pe afirmatii pur si simplu, si deci pe credinta ca maestrii au demonstrat anumite afirmatii? Pina la urma chiar matematica ar fi cea mai indreptatita sa se bazeze doar pe afirmatii de vreme ce ele nu fac rau nimanui si nici nu au implicatii sociale sau umane directe. Si totusi nu o face: desi obiectele studiului matematicienilor sint transcendente, matematicienii nu sar peste etape, ci merg din aproape in aproape cu gindirea.

Asa ar trebui facut si in ceea ce priveste cunoasterea lui Dumnezeu: nu poti pretinde ca ai inviat de vreme ce nu ai depasit nici macar cele mai comune incercari omenesti. Vorbesti despre iubire dar habar nu ai ce inseamna sa fii nu doar trist, ci batrin si bolnav, disperat, vorbesti despre inviere si despre viata vesnica dar faci guturai ca toata lumea si vrei sa fii crezut inclusiv cind vorbesti despre vindecari miraculoase.
Fireste ca invierea este posibila, nu aceasta este hiba. Hiba este ca, din pacate nici aici criteriul nu este adevarul: criteriul e (tot) supravietuirea (cu orice pret), iar “logica” ar fi cam asa; daca timp de generatii a supravietuit ideea ca Iisus a inviat, atunci e musai ca invierea a avut loc, totul este sa se perpetueze pe mai departe credinta asa cum a fost mostenita.

Convingerea mea este ca o religie (moderna) nu ar trebui sa aiba drept fundament fapte, intimplari din trecut, fie acestea miraculoase ori nu, si nici revelatii. In ciuda aparentelor, ramin suficienti piloni de sprijin si destule caramizi pentru orice constructie de acest tip. Desigur, stiinta este unul dintre piloni: n-as fi sigur insa ca liantul sau caramizile ar putea fi constituite de ideologia aceasta a iubirii dezvoltate de crestini.

Argumentul este unul de acelasi grad utopic si de abstractizare ca acela al iubirii universale impuse de crestini. Daca exista in universul acesta colosal, undeva la o departare foarte mare si altfel de fiinte inteligente, foarte diferite de oameni, ar insemna sa practic o discriminare evidenta daca nu le-as iubi la fel si pe ele si m-as rezuma la iubirea fata de aproape (i.e. semeni, inclusiv dusmani): dar cum as putea oare iubi o fiinta pe care inca n-am vazut-o, n-am cunoscut-o, si pe care, probabil nu o voi vedea si nici nu o voi cunoaste nemediat vreodata?

Altfel: daca fiintele respective ar fi constituite din elemente de natura diferita (noi sintem alcatuiti preponderent din apa, sa zicem ca ele ar fi alcatuite din foc, adica plasma), cum as putea oare sa ma apropii de natura lor si sa inteleg ce traiesc ele fara a-mi pune totusi viata in pericol?

Alt argument. Se spune adesea despre modern ca e schizoid. Asta inseamna ca el nu mai poate fi luat ca un intreg: mai mult, nu e deloc evident ca omul vechi ar fi fost structurat altfel. Ei bine, asta inseamna nici mai mult nici mai putin ca in om traiesc mai multe fiinte. Ce reprezinta in acest caz iubirea daca ne gindim la acele fiinte: cine si cum ar trebui sa se ingrijeasca de ele ca sa nu apara abuzuri? Daca una dintre acele fiinte moare, va mai invia si ea? Dar daca unele dintre acele fiinte sint malefice, ce ar avea de facut omul care le traieste?

Probabil ca un crestin autentic ar considera genul acesta de probleme ca fiind simple bazaconii: ei bine, asa vad si eu iubirea universala!

Inapoi la matematica

Doua link-uri interesante:
Liviu Ornea, De ce sa ne placa matematica?
George Lusztig, A descoperi ceea ce preexista - interviu de Liviu Ornea

Henry Poincaré isn't the father of Chaos

... like some people said.
Science means indeed order. Therefore, it is a stupid thing to say that science studies chaos.

"Science is constructed from facts just as a house is constructed from stones, but an accumulation of facts is no more a science than a pile of stones is a house." Henry Poincaré - Science and Hypothesis (1902)